将数字1--8分别填入四面体(如图,由四个三角形组成的立体叫四面体)各圆圈中,使每一个面上四个圆圈中的数字之和相等。

答案及解题思路

由于四面体的四个顶点的四个圆圈都处于三个不同的面,所以相加时每个顶点的数都加过三次。如果设四个顶点所填的数分别为A、B、C、D,那末由1＋2＋3+4+5+6+7+8=36,可得四个面上的数字之和为2(A+B＋C+D)+36。这个和又必须被4整除,因此A+B+C＋D必须被2整除,也就是必须为偶数。

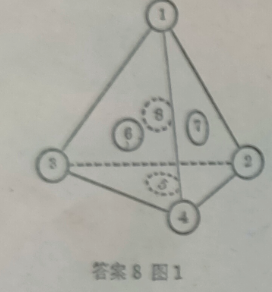
现取最小的四个数1、2、3、4分别为A、B、C、D,那末每一面上四个数字的和为[2(1+2+3＋4)+36]÷4=14。而将1、2、3、4都填入四个顶点后,每个面上三个数都已确定,从而可很容易地求出第四个数，然后填入圆圈，得到一个解答(图1)。

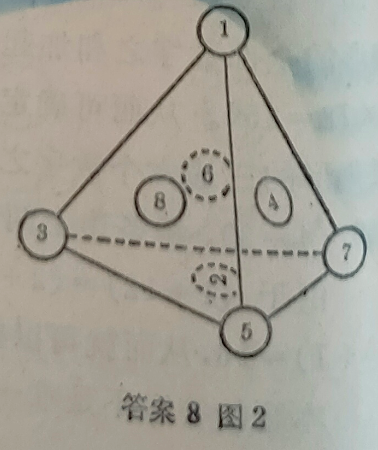
由于A＋B＋C+D为偶数,所以这四个数只能是四个奇数,两奇两偶(如上面的1、2、3、4)，四个偶数三种情况。如取四个奇数,那只能是1、3、5、7。这时,每一面上的四个数字之和为[2(1+3+5+7)+36]÷4=17。将1、3、5、7填入四个顶点后,每个面上有三个数都已确定,从而可以求出第四个数,这样就可以得到第二种解答(图2)。

按照同样的方法进行分析,还可得到其他的答案,少年读者可再试试看。

标签： 奥数有趣的数学易错题趣味题附加题填数